|
I metodi di scheduling, in congiunzione con le tipiche
tecniche di ottimizzazione, possono risolvere efficientemente problemi
complessi, ove l'attuazione di un solo metodo non sarebbe sufficiente.
 e
tecniche di scheduling possono essere combinate con altre tecniche di
ottimizzazione, al fine di risolvere complessi problemi che necessitano
di una riformulazione e quindi di un'applicazione di più metodi
per pervenire alla soluzione. e
tecniche di scheduling possono essere combinate con altre tecniche di
ottimizzazione, al fine di risolvere complessi problemi che necessitano
di una riformulazione e quindi di un'applicazione di più metodi
per pervenire alla soluzione.
In generale, la rappresentazione logica della teoria dei grafi può
essere ottimamente combinata con quella dello scheduling, ottenendo una
semplificazione della trattazione del problema.
Ad esempio, la tipica rappresentazione di un problema di schedulazione
è quella della rappresentazione dei carichi con delle barre, in
cui viene rappresentato il tempo processore a disposizione, o orizzonte
di processamento, mentre le singole barre rappresentano di fatto i task
da schedulare. Tali informazioni possono essere riportate all'interno
di un apposito grafo nel quale i rami rappresentano i task, i pesi definiti
sui singoli rami rappresentano il tempo di processamento di ogni task
ed ogni singolo nodo rappresenta il cambio di sequenza da un task ad un
altro. Quindi, la numerazione dei singoli nodi è pari alla numerazione
dei singoli task. Si consideri allora la Fig.1, in cui devono essere processati
6 task, con il vincolo di assenza di preemption; per tale vincolo i possibili
cambi di sequenza possono essere 5. Le quantità intere riportate
sui singoli rami sono i singoli tempi di processamento dei task. In base
a tale rappresentazione è possibile formulare una vasta tipologia
di problemi.
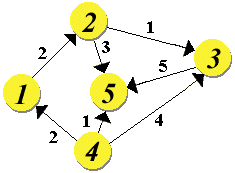
Fig.1: La tipica struttura
a grafo orientato
pesato: essa può rappresentare una sequenza di
task ed i relativi cambi.
MINIMIZZARE IL MAKESPAN
I diversi algoritmi di schedulazione sono preposti alla
determinazione di una o più misura di performance, cioé
minimizzare la massima lateness, o minimizzare i costi/tempi di set-up,
o ancora minimizzare il makespan. Con il termine makespan si indica la
massima lunghezza della schedula; in questo caso si desidera minimizzare
la lunghezza totale della sequenza ammissibile di task, cioè si
desidera ottenere una sequenza la cui lunghezza sia minima.
Per ottenerer una simile misura di prestazione, si può utilizzare
un algoritmo tipico della teoria dello scheduling oppure si può
tentare di adattare alcune tipiche tecniche di scansione dei grafi per
pervenire a tale misura. L'algoritmo che maggiormente può adattarsi
al problema è quello del minimo albero ricoprente o minimo spanning
tree.
Sia dato un grafo orientato pesato, la cui definizione è la seguente:
"Si definisce grafo pesato orientato una struttura
G(N, A), con N insieme dei nodi e cardinalità | N |,
ed A insieme degli archi e cardinalità | A |. L'insieme
degli archi, A, è caratterizzato da un orientamento a nodo origine
ad uno destinazione i,j".
Quindi il problema del minimo spanning tree può essere
così enunciato:
"Sia dato un grafo orientato pesato G(N, A), con
un insieme di interi senza segno definito sugli archi, allora l'obiettivo
è quello di determinare una struttura che connetta tutti i nodi
del grafo con archi di peso minimo".
Un albero ricoprente di costo minimo è una struttura
che un unico nodo origine, detto radice, ed una serie di ramificazioni;
il cammino in esso individuabile è composto da tutti i nodi del
grafo origine, ma in una sequenza tale per cui la somma dei pesi sui rami
sia minima.
Risulta chiaro, allora, che la determinazione di un minimo spanning tree
induce alla determinazione del makespan minimo.
Un tipico algoritmo per la determinazione dell'albero minimo ricoprente
è quello di Kruskal; di seguito ne sono riportate le parti più
salienti:
| while (archi_trovati < n-1 && prossimo_arco <= numero_archi) |
| //si consideri il prossimo arco |
| from = archi[prossimo_arco].end1; |
| to = archi[prossimo_arco].end2; |
//determina l'assenza di cicli |
| group_from = group[from]; |
| group_to = group[to]; |
if(group_from != group_to) |
| //
non esistono cicli |
| lunghezza_totale = lunghezza_totale + archi[prossimo_arco].lunghezza; |
| archi_trovati = archi_trovati+1; |
| //aggiornamento del numero degli archi che entrano |
| //nella soluzione, e degli elementi che compongono l'albero |
| for(j = 1; j <= n; j++) { |
| if(group[j] = = group_to) |
| group[j] = group_from; |
| prossimo_arco = prossimo_arco + 1; } |
| esiste_albero = archi_trovati + 1; |
Nell'algoritmo vengono considerate alcune strutture dati
(vettori) per la conservazione dei nodi e dei pesi intermedi. L'utilizzazione
congiunta di queste metodologie può essere di valido ausilio ad
esempio per uscire da un labirinto.
LABIRINTI E PROCESSORI
Si consideri un tipico labirinto, all'interno del quale
vengono predisposti degli oggetti, che possono essere dei job da assemblare
al fine di ottenere un oggetto finito. Si è certi che l'insieme
degli oggetti sia disposto lungo il percorso che unisce l'ingresso e l'uscita
del labirinto, paragonabilmente ad una traccia per l'orientamento nel
labirinto. Tali oggetti godono, inoltre, delle seguenti proprietà:
- sono di peso diverso;
- sono dotati di una diversa fase di lavorazione e di un differente
tempo di processamento;
- non è assegnata una rigida sequenza di assemblaggio finale.
Allora il problema può essere così formulato:
un operatore deve assemblare un prodotto, le cui parti componenti sono
i task, la cui struttura è stata precedentemente descritta, impiegando
un tempo minimo. Si tratta cioè di determinare una sequenza di
task che minimizzi il tempo di completamento.
I task però sono disposti all'interno di un labirinto, con coordinate
che congiungono entrata ed uscita. Inoltre, l'operatore è dotato
di un contenitore per la raccolta dei task la cui capienza non è
sufficiente a trasportare tutti i task con un unico prelievo.
Risulta quindi chiaro che la risoluzione ottima del problema si ottiene
per combinazione di una serie di metodologie ed algoritmi noti, quali
ad esempio i grafi, il Knapsack e gli algoritmi di scheduling.
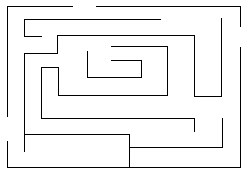
Fig.2: Il labirinto
è la struttura che meglio si
presta alla modellizzazione a grafi. Il cammino in
esso può essere evidenziato da una serie di
marcature/task.
LA RISOLUZIONE
Dalla formulazione del problema, riportata nella precedente
sezione, è chiaro che è indispensabile richiamare alcuni
concetti fondamentali.
Si consideri il labirinto riportato in Fig.2. Tale schema può essere
rappresentato secondo una struttura a Grafo orientato. Passo fondamentale
è quello dell'individuazione degli elementi all'interno di un labirinto.
L'individuazione di tali elementi si può ottenere seguendo almeno
due tecniche:
- determinazione del percorso;
- individuazione degli elementi secondo una tecnica di backtacking.
Se si sceglie il primo approccio, si dovrà utilizzare un metodo
di ricerca del percorso: una tecnica simile è di seguito riportata:
| BOOL Cammino(const Grafo &G, int v, int w, Lista &Cammino) |
| { |
| // utilizzare una struttura a pila per conservare
i cammini intermedi |
| Pila P; |
| int u, x; |
| array prec (G.n()) |
| for (u = 1; u <= prec.n(); u++) |
| // inizializzazione
dell'array di precedenti |
| prec[u] = 0; |
| P.InserisciPila(v); |
| prec[v] = v; |
| BOOL Trovato = False; |
| G.PrimoAdiac(v); |
| while (!P.PilaVuota() && !Trovato) |
| { |
| x = P.CimaPila(); |
| u = G.CorrAdiac(x); |
| while (G.Nodo(u)
&& (prec[u] != 0)) |
| u
= G.succAdiac(u); |
| if (!G.Nodo(u)) |
| P.FuoriPila(); |
| else |
| { |
| P.InserisciPila(u); |
| G.SuccAdiac(x); |
| G.PrimoAdiac(u); |
| if
(u = = w) |
| Trovato
= True; |
| } |
| if (Trovato) |
| do |
| { |
| cammino.InserisciInLista(w); |
| u
= w; |
| w
= prec[w]; |
| } |
| return
Trovato; |
| } |
| } |
Come è possibile notare, la strategia è quella di determinare
le coordinate di ogni singolo nodo del cammino all'interno del labirinto/grafo.
Le singole coordinate vengono poi conservate all'interno di una lista
che sarà disponibile per il prosieguo della procedura.
All'interno della lista, non sono soltanto riportate le coordinate dei
singoli pezzi ma anche i relativi pesi e le informazioni inerenti alla
fase di lavorazione. Individuato il cammino all'interno del labirinto,
si dovranno operare a questo punto, una serie di scelte inerenti le estrazioni
da effettuare, cioè: da quale pezzo incominciare la successiva
fase di lavorazione? In questo caso sarà opportuno operare una
semplificazione del problema di partenza, ciò in quanto una sua
trattazione rigida imporrebbe la costruzione di una serie di vincoli aggiuntivi,
elevando ulteriormente il costo computazionale della soluzione. Tale necessità
è determinata dalle seguenti ragioni:
- La strategia di scelta dei pezzi dovrebbe essere effettuata in relazione
alla sequenza ottima che minimizza il makespan, ai pesi degli oggetti,
ai tempi di processamento.
La soluzione più logica sembrerebbe quella di applicare subito
e direttamente un tipico algoritmo della bisaccia o knapsack per poi impiegare,
banalmente l'algoritmo della schedulazione. Questo modo di procedere sarebbe
però fuorviante, ciò in quanto l'applicazione a priori dell'algoritmo
di Knapsack restituirebbe solo una sequenza di relazione ad alcuni parametri;
probabilmente non sarebbe la sequenza che ottimizza la schedula.
Allora la logica più efficace è quella di utilizzare prima
un algoritmo in modo fittizio che restituisca la sequenza di maespan.
Utilizzando questo vincolo si potrà allora costruire il sacco,
che non sarà quello ottimo, ma che sarà ammissibile per
ottenere il risultato finale, ovvero la schedula ottima. Si immagini di
voler processare gli n task su m macchine parallele, con vincolo di preemption,
al fine di minimizzare il makespan. Quindi sia:
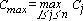
il massimo tempo di completamento (in questo caso può anche essere
interpretato come l'istante in cui tutte le macchine hanno completato
il proprio lavoro).
Mediante il meccanismo dell'interruzione, ogni job può essere processato
su più macchine, purché non simultaneamente, in altri termini,
il job i potrebbe iniziare il suo processamento sulla macchina
i per continuare, successivamente, sulla stessa macchina o su qualunque
altra macchina, eventualmente con ulteriori interruzioni. Si consideri
allora:
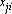 = frazione
di job j processata sulla macchina i = frazione
di job j processata sulla macchina i
ed il seguente vincolo:
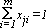
Con tale definizione delle variabili, il tempo totale di lavoro della
i-esima macchina si può esprimere nel seguente modo:
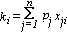
il problema quindi può essere formulato come:
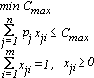
Si noti che non è consentita la preemption, il problema potrà
essere formulato in maniera analoga, ma bisognerà cambiare il vincolo
sulla variabile decisionale: sarà quindi 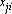 = {0,1}, con variabili binarie ed il vincolo
= {0,1}, con variabili binarie ed il vincolo 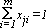 esprimerà il fatto che ogni job può essere processato da
una sola macchina. È possibile dimostrare la seguente affermazione
per il problema precedentemente formulato:
esprimerà il fatto che ogni job può essere processato da
una sola macchina. È possibile dimostrare la seguente affermazione
per il problema precedentemente formulato:
- Se esiste una soluzione ammissibile in corrispondenza della quale
tutti i vincoli di diseguaglianza siano soddisfatti come uguaglianze;
sia x^, allora tale soluzione sarà ottima (x^=x*).
Infatti, rispetto a x^, tutte le macchine hanno lo stesso carico di lavoro
e terminano nel medesimo istante 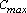 ;
se per assurdo la soluzione ottima fosse x*<>x^, con carico di lavoro
sbilanciato sulle macchine, sarebbe sempre possibile ridurre il valore
del makespan, ridistribuendo opportunamente tra le macchine parte dei
jobs assegnati a quella più carica. Ciò sarebbe però
in contraddizione con l'ottimalità di x*. ;
se per assurdo la soluzione ottima fosse x*<>x^, con carico di lavoro
sbilanciato sulle macchine, sarebbe sempre possibile ridurre il valore
del makespan, ridistribuendo opportunamente tra le macchine parte dei
jobs assegnati a quella più carica. Ciò sarebbe però
in contraddizione con l'ottimalità di x*.
La soluzione ottima del problema si ottiene sommando tra loro i vincoli
sulle macchine e tenendo conto dei vincoli sui jobs, ottenendo così
la seguente posizione:
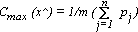
Il vettore delle variabili decisionali x^ fornirà quindi
la sequenza ottima per minimizzare il 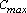 . .
Trovato tale valore, sarà possibile passare alla determinazione
del Knapsack. Il problema, però, è che l'operatore non ha
a disposizione un sacco di capienza sufficiente al trasporto di tutti
gli oggetti in un unico viaggio, quindi l'azione sarà quella di
entrare ogni volta nel labirinto con l'aiuto della lista delle coordinate.
Il vettore delle sequenze di processamento, all'interno, non potrà
prelevare gli oggetti così come gli vengono proposti, ma dovrà
estrarli secondo una procedura Knapsack, tenendo conto che non potranno
essere trasportati tutti gli oggetti in un unico viaggio. Il problema,
come già più volte evidenziato, può essere formulato
nel seguente modo. Si hanno a disposizione n oggetti, ciascuno con valore
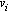 e costo e costo
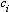 ; nella
fattispecie, tali parametri possono essere rivisti come tempo di processamento
e peso. In questo caso il problema può essere espresso come massimizzazione
del valore, nel rispetto della sequenza makespan e minimizzazione del
peso, visto che dovranno essere effettuati diversi viaggi. Se C è
la disponibilità massima del trasporto, si avrà: ; nella
fattispecie, tali parametri possono essere rivisti come tempo di processamento
e peso. In questo caso il problema può essere espresso come massimizzazione
del valore, nel rispetto della sequenza makespan e minimizzazione del
peso, visto che dovranno essere effettuati diversi viaggi. Se C è
la disponibilità massima del trasporto, si avrà:
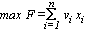
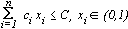
quindi in corrispondenza di tutte le variabili che assumono valore 1;
allora, il corrispondente oggetto entrerà nella soluzione e quindi
nel sacco.
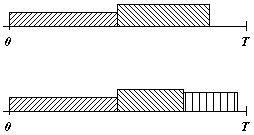
Fig.3: L'intervallo
O - T rappresenta l'orizzonte
temporale in cui avviene il processamento
dell'intera sequenza. Tale risorsa di tempo viene
solitamente suddivisa tra i vari task.
Per una fattiva implementazione del problema di Knapsack,
si consideri una struttura di oggetti, con i campi che riportano le informazioni
fondamentali quali l'indice, indispensabile per la sequenza, il peso,
le coordinate, il tempo.
Si avrà:
| Soluzione Knapsack (array oggetti, int C) |
| { |
| int n = oggetti.n(); |
| array Fk(C + 1); |
| for (int j = 1; j <= C + 1; j++) |
| Fk[j] = 0; |
| matrix xk(C + 1, n); //
allocare una matrice di booleani |
| for (j = 1; j <= C + 1; j++) |
| for (int i = 1;
i <= n; i++) |
| xk[j][i]
= FALSO; |
| for (int k = 1; k <= n - 1; k++) |
| for (int j = C +
1; j > oggetti[i].c; j--) |
| if
(Fk[j - oggetti[k].c] + oggetti[k].v > Fk[j]) |
| { |
| Fk[j]
= Fk[j - oggetti[k].c + oggetti[k].v; |
| for
(int i = 1; i <= k - 1; i++) |
| xk[j][i]
= xk[j - oggetti[k].c][i]; |
| xk[j][k]
= TRUE; |
| } |
| // calcola la soluzione |
| Soluzione S; |
| if (oggetti[n].c <= c && Fk[C
+ 1 - oggetti[n].c + oggetti[n].v > Fk[C + 1]) |
| // scegli gli elementi soluzione che non
violano |
| // il vincolo di capacità |
| } |
Perciò mediante l'applicazione di tale algoritmo,
sarà possibile determinare, di volta in volta, gli oggetti che
devono essere prelevati dal labirinto e posti in fase di processamento.
L'azione dinamica si può espletare nel seguente modo:
- determinare il cammino e la lista di oggetti;
- implementare il makespan e determinare la sequenza di schedulazione;
- entrare nel labirinto e con la procedura di knapsack riempire il sacco,
uscire ed avviare il processamento; mentre ciò avviene, rientrare
nel labirinto e prelevare un altro sottoinsieme di oggetti fintantochè
tutti gli oggetti non sono stati rimossi dal labirinto stesso.
Un'ulteriore complicazione può essere data dall'inserimento nel
vincolo di rispetto della sequenza, e che negli intervalli di tempo in
cui l'operatore sta asportando gli oggetti dal labirinto, almeno un processamento
sia in atto; cioè l'insieme delle macchine non deve mai essere
inoperoso. Chiaramente tale imposizione complica notevolmente la soluzione
del problema.
CONCLUSIONI
Le tecniche di ottimizzazione congiunte spesso vengono utilizzate per
risolvere problemi complessi che non ricadono in una branca specifica
dell'ottimizzazione.
L'esempio riportato nelle precedenti sezioni può fattivamente prestarsi
come implementazione di un gioco. La logica fondamentale è quella
di riuscire a customizzare le diverse tecniche e a fonderle per ottenere
la soluzione ottima di un particolare problema.
 NOTE:
NOTE:
Cammino minimo
La procedura cammino ha complessità nell'ordine 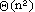 .
Tale complessità è sostanzialmente determinata dalla scansione
delle strrutture aggiuntive al fine di ottenere la migliore sequenza di
visita degli elementi. Nel caso invece di determinazione di un cammino
ottimale, la computazione della complessità, sia essa spaziale
che temporale, deve ovviamente variare, tenendo conto cioè dei
vincoli del problema e della dimensione dell'input. .
Tale complessità è sostanzialmente determinata dalla scansione
delle strrutture aggiuntive al fine di ottenere la migliore sequenza di
visita degli elementi. Nel caso invece di determinazione di un cammino
ottimale, la computazione della complessità, sia essa spaziale
che temporale, deve ovviamente variare, tenendo conto cioè dei
vincoli del problema e della dimensione dell'input.
Complessità di knapsack
La complessità spaziale dell'algoritmo di knapsack è in
generale, dell'ordine di 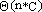 ,
mentre quella temporale è nell'ordine di ,
mentre quella temporale è nell'ordine di 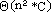 ,
nei casi peggiore e medio, mentre sarà nell'ordine ,
nei casi peggiore e medio, mentre sarà nell'ordine 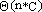 nel caso migliore; ciò in quanto si dovrà fare riferimento
ai tre cicli di for innestati, con quello esterno che deve essere eseguito
per n volte. Le complessità espresse sono però falsamente
polinomiali. Infatti C fa parte dell'input e lo spazio richiesto per la
sua memorizzazione è:
nel caso migliore; ciò in quanto si dovrà fare riferimento
ai tre cicli di for innestati, con quello esterno che deve essere eseguito
per n volte. Le complessità espresse sono però falsamente
polinomiali. Infatti C fa parte dell'input e lo spazio richiesto per la
sua memorizzazione è: 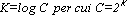 . .
Assegnamento generalizzato
Eliminando il vincolo di preemption dalla determinazione del makespan,
si ottiene un tipico problema di assegnamento generalizzato, così
detto perché più jobs possono essere assegnati ad una stessa
macchina, come risulta dal primo gruppo di vincoli caratteristici della
formulazione del problema, mancando la corrispondenza 1-1 come nel problema
di assegnamento classico. Il problema di assegnamento generalizzato è
un tipico problema NP-HARD.
L'albero ricoprente
La complessità dell'algoritmo per la determinazione del minimo
albero ricoprente è dell'ordine di 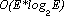 ,
ciò in quanto per ogni arco sono richieste n operazioni per aggiornare
il gruppo di connessioni. Soo questa parte dell'algoritmo ha complessità
dell'ordine di ,
ciò in quanto per ogni arco sono richieste n operazioni per aggiornare
il gruppo di connessioni. Soo questa parte dell'algoritmo ha complessità
dell'ordine di 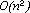 .
Il ciclo innescato per tutti gli archi richiede O(E) operazioni. Pertanto
la complessità effettiva dipende sostanzialmente dalla densità
degli archi; quindi se esistono pochi archi .
Il ciclo innescato per tutti gli archi richiede O(E) operazioni. Pertanto
la complessità effettiva dipende sostanzialmente dalla densità
degli archi; quindi se esistono pochi archi 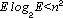 ,
l'aggiornamento del gruppo delle connessioni è il fattore predominante.
Se invece il grafo è denso sarà il primo termine a dominare. ,
l'aggiornamento del gruppo delle connessioni è il fattore predominante.
Se invece il grafo è denso sarà il primo termine a dominare.
|

